学会分类分步解排列组合题
说到行测排列组合问题,其本质上还是计数问题。一些简单题目可以通过枚举法进行计数,但是遇到稍微复杂的题目同学们就会感到束手无策,复习过程中总有种吃力不讨好的感觉。但其实想攻破排列组合并不难,关键在于理解分类分步的含义,并且能够在题目中正确运用。
分类:做事时可分不同类别的方法去做,且每一类的方法均能完成此事。在计算结果时,将每一类方法数相加,即为完成这件事的方法数。比如小明要从A地前往B地,可供选择的交通方式有2列不同班次的火车和3趟不同班次的大巴,均能完成任务,结合分类相加的计算方法可得共有2+3=5种方法。
分步:做事时分不同步骤去做,所有步骤完成后才能完成此事。在计算结果时,将每一步方法数相乘,即为完成这件事的方法数。再比如小明要从A地前往B地,中途需要在C地转车,从A地到C地有2趟火车,从C地到B地有3趟大巴,结合分步相乘的计算方法可得共有2×3=6种。
【例1】单位3个科室分别有7名、9名和6名职工。现抽调2名来自不同科室的职工参加调研活动,则有多少种不同的挑选方式?
A.146
B.159
C.179
D.286
答案:B
【解析】抽调情况为抽调两个科室且每个科室各抽调1人,假设这三个科室分别是A、B和C,首先根据抽调科室可分为三类:①A和B;②A和C;③B和C,其次计算每一类的方法数,①A和B:从A科室抽调1人,有7种选择,从B科室抽调1人,有9种选择,从A抽调、从B抽调两者缺一不可,故属于分步思维,方法数为7×9=63种;同理计算②A和C:7×6=42;③B和C:9×6=54。最后将三类方法数相加,则有63+42+54=159,正确答案为B。
【例2】某企业国庆放假期间,甲、乙和丙三人被安排在10月1号到6号值班。要求每天安排且仅安排1人值班,每人值班2天,且同一人不连续值班2天。问有多少种不同的安排方式?
A.15
B.24
C.30
D.36
答案:C
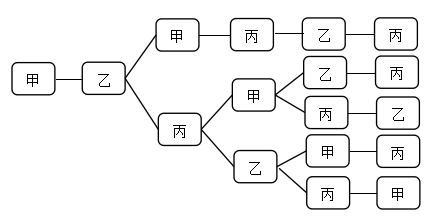
【解析】根据题意需要安排甲乙丙三人在10月1号到6号值班,6天中每天安排1人,每人值班2天且不连续。那么第一步可以先安排1号,甲、乙、丙三人选一人值班,有3种选择。第二步安排2号,由于每人值班不连续,所以从剩下两人中选一人,有2种选择。第三步安排3-6号,安排3号值班的人可以和1号值班的人相同,也可以和1号、2号值班人员均不同,而3号值班的人是否和1号值班人员相同,会影响后面日期的安排,所以需分类讨论。假设1号安排甲,2号安排乙(如下图所示),则3号安排分两类:①安排甲;②安排丙。计算每一类方法数:①安排甲:根据题干条件,4号只能安排丙,5号安排乙,6号安排丙,有1种情况。②安排丙:4号可以安排甲或者乙,若4号安排甲,5号可以安排乙或者丙,6号即为剩下一人值班,有2种;同理,若4号安排乙,5号可以安排甲或者丙,6号也是剩下一人值班,有2种,则共有2+2=4种,则第三步共有1+4=5种。最终分步相乘3×2×5=30种,正确答案为C。

点击分享此信息:





